Introduction
This blog introduces the bigram model for word segmentation.
So the bigram model considers previous character which makes more sense in terms of context. The equation should be:
\(P(W_{i}|W_{i-1})=\frac{C(W_{i},W_{i-1})}{C(W_{i-1})}\) However, we may also wonder what if $W_{i-1}$ is zero? The probability cannot be computed in this case. The combination of $W_{i}$ and $W_{i-1}$ can be zero as well.
Witten-Bell smoothing
Thus, to solve this problem, we need some smoothing and interpolation is introduced. \(P^{'}(W_{i}|W_{i-1})=\frac{C(W_{i-1})}{N_{1+}(W_{i-1})+C(W_{i-1})}*P(W_{i}|W_{i-1})+\frac{N_{1+}(W_{i-1})}{N_{1+}(W_{i-1})+C(W_{i-1})}*P(W_{i})\) source
This smoothing trick combines both bigram and unigram. There are two coefficient, $\lambda_{1}$ and $\lambda_{2}$. First, we make sure $\lambda_{1}+\lambda_{2}=1$ and the $\lambda$ decides which part contributes more to the final probability. Here $N_{1+}(W_{i-1})$ means words following $W_{i-1}$ at least once. In fact, it measures the freedom/flexibility of collocation. For example, Hong Kong, so the word following Hong is mainly Kong. In this case, the collocation is very strong and the proportion of $W_{i}$ as an independent word should be lower, and the conditional probability therefore becomes higher. That is to say, the word is quite dependent on its previous word. Another example, red apple. Since red is just an adjective and almost any nouns can be modified by it. The value of $N_{1+}(W_{i-1})$ is supposed to be pretty high. More importantly, if the value of conditional probability is zero, we still have unigram part so that the probability won’t be zero. Of course, in terms of preventing the $C(W_{i-1})$ from being zero, plus 1 can easily fix it.
So far the probabilities are calculable. The workflow would be like (赫尔辛基大学在芬兰[The university of Helsinki is in finland/Helsingin yliopisto on suomessa]): 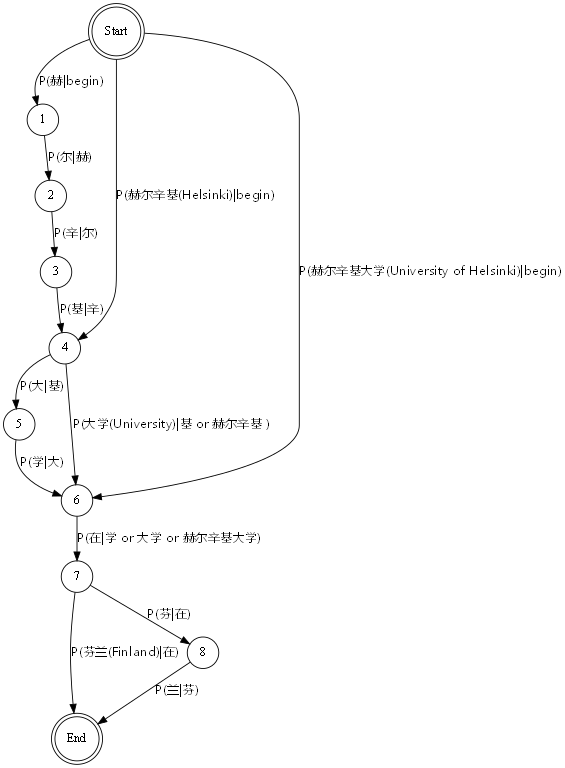
Find best segmentation way
Yes, next step requires ability to search for the optimal path in this graph. Probabilities will serve as weights of edges.
In practice, adding regular expression would be a good idea to recognize time and numbers, boosting the performance on OOV(out of vocabulary). Implementation is in the repository. The blog is just complementary to the code.
Here we can also see some drawbacks of this approach:
- It relies on large training data.
- N-gram usually performs better as N grows but also more computationally expensive.
- It still can’t deal with unseen words which never appear in training data. (Regular expression only helps some but can’t manage person’s name)
HMM model seems to be more effective in tackling OOV.
Reference: Speech and Language Processing