About Graph, there are several basic concepts:
- Node, as a point in the graph.
- Edge/Arc, meaning two nodes are connected.
- Weight, the value/expense of edge.
- Path, the way including all passed nodes from one node to the target one.
- Cycle, if the path starts from one node and end with the same.
- Directed Graph, edges have direction, pointing to certain node.
- Adjacency matrix, if the graph is not directed then the matrix is symmetric.
With networkx package, it’s easy to draw some example graphs.
There is an interesting topic about Graph: Knight’s Tour Problem. But it will not be covered in this post.
I want to introduce two algorithms of finding the shortest path. That’s to discover the way at lowest cost.
Dijkstra’s algorithm
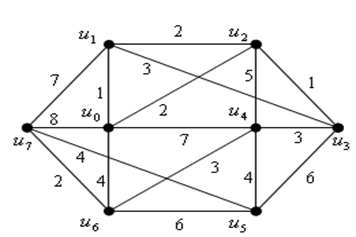
The problem is that we need to find the cheapest way from node 0 to other nodes.
First we need to build an adjacency matrix and then to iteratively travel each point.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
"""
Dijkstra Algorithm
"""
oo=float('inf')
#adjacency matrix
distant = [[oo,1,2,oo,7,oo,4, 8],#
[1,oo,2,3,oo,oo,oo,7],#
[2,2,oo,1,5,oo,oo,oo],#
[oo,3,1,oo,3,6,oo,oo],#
[7,oo,5,3,oo,4,3, oo],#
[oo,oo,oo,6,4,oo,6,4],#
[4,oo,oo,oo,3,6,oo,2],#
[8,7,oo,oo,oo,4,2,oo]]#
S=[0];U=[i for i in range(1,len(distant[0]))]
lowest_cost = {0:0,1:oo,2:oo,3:oo,4:oo,5:oo,6:oo,7:oo}
cost=list(lowest_cost.values())
z = {0:0,1:0,2:0,3:0,4:0,5:0,6:0,7:0}
def dijkstra(distant,n):
iternum=0
while U != []:#as long as the U is not empty
for i in U:#for each element in U
if lowest_cost[i]> lowest_cost[S[iternum]]+distant[S[iternum]][i]:#if the cost is lower than two plus together, it'll be recorded as a new lowest cost
lowest_cost[i]=lowest_cost[S[iternum]]+distant[S[iternum]][i]
cost[i]=lowest_cost[i];z[i]=S[iternum]
else:
pass
#always choose the minimum cost and restore it
picked = min(cost[1:n+1])
found_number = cost.index(picked)
cost[found_number]=oo#reset as infinitive for next round selection
U.remove(found_number)
S.append(found_number)
iternum +=1
return lowest_cost
dijkstra(distant,7)
for i in range(len(cost)):
print("Node({0}) to Node 0 has shortest path at expense of:{1}".format(i,lowest_cost[i]))
print('The best previous node of Node({0}) is:{1}'.format(i,z[i]))
Dijkstra algorithm computes the shortest path between a fixed node and all the other nodes. This is very helpful when we deal with some delivery issues, like there is a logistics center.
Floyd algorithm
This algorithm enables us to find the shortest path of any two nodes and record the path (which nodes passed by).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
'''
Floyd Algorithm
'''
import numpy as np
oo=float("inf")#其实把这个调大一点也可以
d_matrix=np.array([[oo,1,2,oo,7,oo,4, 8],# 这边其实就是每个点之间相互的距离
[1,oo,2,3,oo,oo,oo,7],#
[2,2,oo,1,5,oo,oo,oo],#
[oo,3,1,oo,3,6,oo,oo],#
[7,oo,5,3,oo,4,3, oo],#
[oo,oo,oo,6,4,oo,6,4],#
[4,oo,oo,oo,3,6,oo,2],#
[8,7,oo,oo,oo,4,2,oo]])
r_matrix=np.array([[i for i in range(d_matrix.shape[0])]for k in range(d_matrix.shape[0])])
def Floyd(n):
for k in range(n):
for i in range(n):
for j in range(n):
if d_matrix[i][j]>d_matrix[i][k]+d_matrix[k][j]:
d_matrix[i][j]=d_matrix[i][k]+d_matrix[k][j]
d_matrix[j][i]=d_matrix[i][k]+d_matrix[k][j]
r_matrix[i][j]=k;r_matrix[j][i]=k
print(d_matrix)
print(r_matrix)
Floyd(d_matrix.shape[0])
def printpath(r_mx,fromnd,tond):
nextnd=r_mx[fromnd][tond]
pathnd=[fromnd]
while nextnd != tond:
pathnd.append(nextnd)
nextnd = r_mx[nextnd][tond]
pathnd.append(nextnd)
print("Best path from %d to %d"%(fromnd,tond),"->".join([str(i) for i in pathnd]))
printpath(r_matrix,4,1)
With Floyd’s way, we can choose any two nodes and find the shortest way of it. The example from node 4 to 1, the best path is 4->3->1.
The main part of above codes were actually written during my undergraduate study, the course Mathematical Modeling in Economy. The content of it really helped me a lot. The example problem also comes from the course, so I should give credit to it.
So what is the meaning of finding the shortest path? Not only for route planning but even quite useful for NLP, for example word segmentation, syntax parsing!