Credit to Problem solving with algorithms and data structures using Python section 7.5 & 7.6 & 7.7
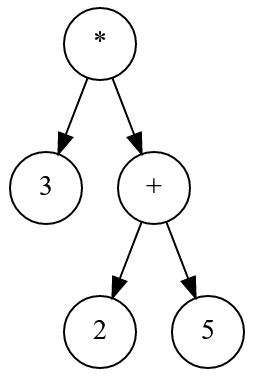
The idea is to use binary tree to parse mathematical tree. For example, (3*(2+5)) the tree should be like:
First we need to have a class for binary tree.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# some may be modified
class BinaryTree:
def __init__(self,rootobj):
self.key=rootobj
self.leftchild=None
self.rightchild=None
def insertLeft(self,newnode):
if self.leftchild==None:
self.leftchild=BinaryTree(newnode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
def insertRight(self,newnode):
if self.rightchild==None:
self.rightchild=BinaryTree(newnode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
def getRightChild(self):
return self.rightchild
def getLeftChild(self):
return self.leftchild
def setRootVal(self,value):
self.key=value
def getroot_value(self):
return self.key
insertLeft()function check if the left subnode exists, if not then create another new Binary tree class as the leftchild node. If there’s already something, then creating a new node and put the original leftchild as the leftchild node of the new one. Now the new Binary tree class is the leftchild node. Same for insertRight().
Then we need to have a function to build a tree and parse this type of expressions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# some lines are modified
def buildParseTree(fpexp):
fplist = [i for i in fpexp]
pStack = []
eTree = BinaryTree('')
pStack.append(eTree) # equuivalent of pushing into stack
currentTree = eTree
for i in fplist:
if i == '(':
currentTree.insertLeft('')
pStack.append(currentTree)
currentTree = currentTree.getLeftChild()
elif i in ['+', '-', '*', '/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.append(currentTree)
currentTree = currentTree.getRightChild()
elif i == ')':
currentTree = pStack.pop()
elif i not in ['+', '-', '*', '/', ')']:
currentTree.setRootVal(int(i))
parent = pStack.pop()
currentTree = parent
else:
raise ValueError("token '{}' is not a valid integer".format(i))
return eTree
import operator as op
def evaluate(tree):
operations={"+":op.add,"-":op.sub,"*":op.mul,"/":op.truediv}
leftC = tree.getLeftChild()
rightC = tree.getRightChild()
if leftC and rightC:
return operations[tree.getroot_value()](evaluate(leftC),evaluate(rightC))
else:
return tree.getroot_value()
def preorder(tree):
if tree:
print(tree.getroot_value())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
preorder(buildParsetree("(3*(2+5))"))
evaluate(buildParseTree("(3*(2+5))"))
The result is 3*7=21 and by preorder function, we have all nodes in the tree which in order are */3/+/2/5. Things seem to have been solved so far. But I wonder if some parentheses are necessary in the expression. Here I have two more examples: 1) 2+(3*5)
2) (3+5)*2
And this time I don’t want the outside parenthesis. In order to do this, I made some modifications:
1
2
3
4
5
6
7
8
elif i not in ["+", "-", "*", "/", ")"]:# number
if currentTree.getroot_value()=="":# number without parentheses
currentTree.insertleft(" ")
node_stack.append(currentTree)
currentTree = currentTree.getLeftchild()
currentTree.setroot(int(i))
parent = node_stack.pop()
currentTree = parent
If the root value is ““(empty string) which means there is no operator encountered, then the number should be automatically put on the left side of current tree. Also, another issue is that if the operator is behind a parenthesis, it will replace the current operator. In this case, the whole subtree should be a leftchild node of a new Binary tree class. So we need to have a new subtree and keep the original one as the leftchild.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# add this function into the BinaryTree class
def replacecurr(self,newnode):
t_r = self.rightchild
t_l = self.leftchild
self.leftchild = BinaryTree(self.key)
self.rightchild = None
self.leftchild.leftchild = t_l
self.leftchild.rightchild = t_r
#change the buildParseTree function
elif p in ["+", "-", "*", "/"]:
if currentTree.getroot_value() in ["+", "-", "*", "/", ")"]:# calculation symbol but without priority
currentTree.replacecurr(p)
currentTree.setroot(p)
currentTree.insertright(" ")
node_stack.append(currentTree)
currentTree = currentTree.getRightchild()
Thus, the output of 2+(35)=17, and the nodes are +/2/*/3/5. Then the second example (3+5)2=16 and nodes are */+/3/5/2. Good, the uncessary parenthesis issue looks solved. However, I come up with another example, what will happen for 2+(3*5)/3? evaluate(buildParseTree("2+(3*5)/3")) Oops, the result is 5.667. The new problem is that we don’t have any priority for the calculation so the program see the expression as (2+(3*5))/3 which equals to 17/3=5.667
So we need some priorities to put * and \ prior in calculation. The final entire codes will be like:(look kind of messy)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
class BinaryTree:
def __init__(self,rootobj):
self.key=rootobj
self.leftchild=None
self.rightchild=None
def insertLeft(self,newnode):
if self.leftchild==None:
self.leftchild=BinaryTree(newnode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
def insertRight(self,newnode):
if self.rightchild==None:
self.rightchild=BinaryTree(newnode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
def replacecurr(self,newnode):
t_r = self.rightchild
t_l = self.leftchild
self.leftchild = BinaryTree(self.key)
self.rightchild = None
self.leftchild.leftchild = t_l
self.leftchild.rightchild = t_r
def getRightChild(self):
return self.rightchild
def getLeftChild(self):
return self.leftchild
def setRootVal(self,value):
self.key=value
def getroot_value(self):
return self.key
def buildParseTree(fpexp):
fplist = [i for i in fpexp]
pStack = []
eTree = BinaryTree('')
pStack.append(eTree) # equuivalent of pushing into stack
currentTree = eTree
for i in fplist:
if i == '(':
currentTree.insertLeft('')
pStack.append(currentTree)
currentTree = currentTree.getLeftChild()
elif i in ["+", "-"]:
if currentTree.getroot_value() in ["+", "-", "*", "/", ")"]:# calculation symbol but without priority
currentTree.replacecurr(i)
currentTree.setRootVal(i)
currentTree.insertRight(" ")
pStack.append(currentTree)
currentTree = currentTree.getRightChild()
elif i in["*", "/"]:
if currentTree.getroot_value() in ["+", "-", "*", "/", ")"]:# calculation symbol but without priority
pStack.append(currentTree)
currentTree = currentTree.getRightChild()
currentTree.replacecurr(i)
currentTree.setRootVal(i)
currentTree.insertRight(" ")
pStack.append(currentTree)
currentTree = currentTree.getRightChild()
elif i == ')':
currentTree = pStack.pop()
elif i not in ['+', '-', '*', '/', ')']:
if currentTree.getroot_value()=="":# number without parentheses
currentTree.insertLeft(" ")
pStack.append(currentTree)
currentTree = currentTree.getLeftChild()
currentTree.setRootVal(int(i))
parent = pStack.pop()
currentTree = parent
# in case of consecutive operator and can't go back to root node
if currentTree.getroot_value() in ["*","/"] and currentTree.getLeftChild().getroot_value() in ["+", "-", "*", "/", ")"]:
parent = pStack.pop()
currentTree = parent
else:
raise ValueError("token '{}' is not a valid integer".format(i))
return eTree
import operator as op
def evaluate(tree):
operations={"+":op.add,"-":op.sub,"*":op.mul,"/":op.truediv}
leftC = tree.getLeftChild()
rightC = tree.getRightChild()
if leftC and rightC:
return operations[tree.getroot_value()](evaluate(leftC),evaluate(rightC))
else:
return tree.getroot_value()
def preorder(tree):
if tree:
print(tree.getroot_value())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
preorder(buildParseTree("2+(3*5)/3"))
evaluate(buildParseTree("2+(3*5)/3"))
Great! The result is finally correct: 2+5=7.0